Интерфейс пользователя
 |
Несмотря на то, что программа ANSYS располагает богатыми и сложными возможностями, ее организационная структура и “дружеский” графический интерфейс пользователя (GUI) делают изучение и применение программы очень удобным (см. рис 1).
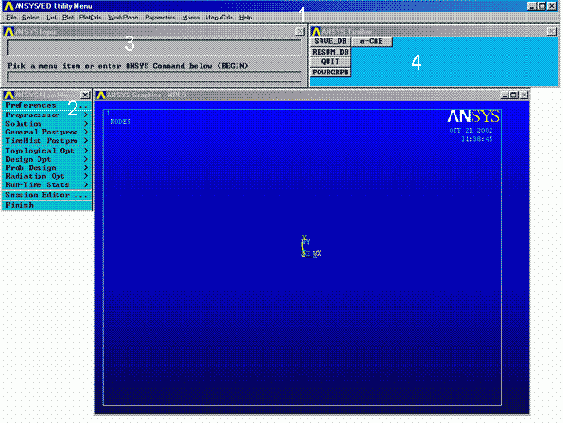
Система меню (на основе разработки фирмы Motif) обеспечивает ввод данных и выбор действий программы с помощью панелей диалога, выпадающих меню и окон списка, помогая пользователю управлять программой.
С помощью этого интерфейса обеспечивается удобный интерактивный доступ к функциям, командам, документации и справочным материалам программы, создается своего рода путеводитель, обучающий пользованию программой шаг за шагом при проведении анализа. В то же время программой предоставляется полная документация в интерактивном режиме и самая современная система HELP на основе гипертекстового представления для помощи опытным пользователям при выполнении сложных видов работ. Система меню наделена “интуитивными” свойствами, помогая пользователю целесообразно управлять программой. Исходные данные можно вводить с помощью манипулятора “мышь”, клавиатуры или сочетая эти два варианта.
Существуют четыре общих метода ввода инструкций для программы, когда используются следующие возможности интерфейса:
· меню;
· панели диалога;
· линейка инструментов;
· непосредственный ввод команд.
Меню
представляет собой перечень нескольких логически связанных процедур управления программой, которые расположены в отдельных окнах. К этим окнам, которые можно переместить или убрать с помощью мыши, доступ возможен в процессе работы. Команды программы объединены в отдельные функциональные группы для быстрого доступа в соответствующие моменты.
Меню утилит (1) – содержит набор часто используемых процедур, которые отображены здесь для доступа в любой момент работы программы. Выполнению этих процедур предшествует появление в каскадном порядке выпадающих меню, которые позволяют непосредственно выполнить нужное действие или перейти в панель диалога. Меню утилит не обладает жестким режимом работы, и пользователь может выполнить несколько действий за одно обращение (например, отказаться от прежнего намерения и перейти к выполнению другой операции).
Главное меню (2) – перечисляет основные функции программы, которые группируются в располагаемые сбоку всплывающие (динамические) меню, вид которых зависит от продвижения по программе.
Окно ввода (3) – представляет собой область для набора команд и показа сообщений-подсказок программы. Имеется возможность обратиться к списку введенных ранее команд. Команды можно извлекать из файла регистрации (log-файла) введенных ранее команд и/или входных файлов для последующего ввода.
Линейка инструментов (4) – дает возможность пользователю разместить обычно используемые процедуры, например, команды или написанные пользователем подпрограммы для быстрого их запуска щелчком мыши. Линейка инструментов является весьма эффективным средством для запуска команд программы, что определяется широкими возможностям ее конфигурирования. Предоставляет пользователю средства создавать кнопки с текстом и иметь немедленный доступ к часто исполняемым командам. Линейка инструментов может вместить до 200 кнопок.
Независимо от того, каким образом заданы команды, они, в конечном счете, используются для передачи всех данных и управления всеми действиями программы. Интерфейс пользователя организован так, чтобы осуществлять выбор и исполнение команд путем удобного и “интуитивного” использования меню, панелей диалога и линейки инструментов.
Интерактивный характер интерфейса и группирование команд по функциональной близости делают прозрачным смысл команд по их краткому синтаксису. Пользователи, знакомые с командами программы, могут вводить их непосредственно с клавиатуры.
Любая однажды выполненная команда записывается в файл регистрации сеанса работы. Доступ к этому файлу возможен из окна вывода, что позволяет обратиться к списку команд в случае ошибки или записать его в виде файла для исполнения в пакетном режиме.
Программа также использует графический индикатор в виде меняющего длину столбика при выполнении потенциально продолжительной процедуры (например, построение сетки). Пользователь имеет возможность остановить такую операцию простым щелчком мыши.
Графическое окно (5) – представляет собой область для вывода такой графической информации, как конечно-элементная модель или графики результатов анализа. Размеры окна можно устанавливать, уменьшая или увеличивая по своему усмотрению.
Окно вывода (не показано) – фиксирует отклик программы на команды и действия пользователя. Всегда доступно при работе интерфейса.
Панель диалога (не показана) – это окно, предоставляющее пользователю на выбор перечень действий для выполнения процедур и установки необходимых настроек. Такие панели подсказывают, какие данные следует вводить и какие решения принимать для определенных процедур.
ПРОЧНОСТНОЙ СТАТИЧЕСКИЙ АНАЛИЗ
Возможности статического прочностного анализа программы ANSYS используются для определения перемещений, напряжений, деформаций и усилий, которые возникают в конструкции или ее составных частях в результате приложения механических сил. Статический анализ пригоден для задач, в которых действие сил инерции или процессы рассеяния энергии не оказывают существенного влияния на поведение конструкции. Такой тип анализа можно использовать во многих приложениях, например, для определения концентрации напряжений в галтелях конструктивных элементов или для расчета температурных напряжений.
Конструкторы и специалисты в области прочности знакомы с этим видом анализа и, вероятно, решали многочисленные задачи статики, используя классические методы или соотношения из соответствующих справочников. В программе ANSYS для решения этих задач используются численные методы. Разрешающее уравнение статического анализа записывается в виде
[K]{u} = {F},
где [K] – матрица жесткостей;
{F} – вектор сил;
{u} – вектор перемещений.
Компоненты вектора сил {F} могут представлять собой сосредоточенные силы, тепловые нагрузки, давления и силы инерции. Можно проводить расчеты по определению таких значений ускорений, которые обеспечивают статическое уравновешивание приложенных к системе нагрузок.
Статический анализ в программе ANSYS может включать такие нелинейности, как пластичность и ползучесть материала, большие прогибы, большие деформации и контактное взаимодействие. Нелинейный статический анализ обычно выполняется при постепенном возрастании нагрузок, чтобы можно было получить верное решение.
Динамика переходных процессов
Анализ переходных процессов (неустановившихся режимов) применяется для определения параметров динамического поведения конструкций, которые подвергаются действию нагрузок, произвольно меняющихся во времени.
Выходные величины полученного решения (в виде узловых перемещений, деформаций, напряжений, усилий и т.п.) представляют собой функции времени. Каждую из этих величин можно вывести на экран в виде графика зависимости от времени или некоторой другой переменной с помощью постпроцессора истории нагружения. Постпроцессор общего назначения позволяет просмотреть результаты анализа переходного процесса для любого момента времени (например, показать картину напряженно-деформированного состояния).
Отклик на гармоническое воздействие
Анализ гармонического воздействия используется для определения параметров установившегося движения линейной системы при синусоидальном силовом возбуждении. Этот вид анализа полезен при исследовании влияния нагрузок, меняющихся во времени по гармоническому закону, типа тех, что испытывают станины и фундаменты оборудования с вращающимися частями.
Перемещения меняются синусоидально с частотой w, но не обязаны совпадать по фазе с вынуждающей силой. Нагрузки могут быть в форме узловых сил, начальных перемещений или распределенными по элементу. Для заданной частоты пользователь имеет возможность найти перемещения либо в виде набора амплитуд и фазовых углов, либо в виде реальной и мнимой частей решения.
Спектральный анализ
Определение спектра отклика конструкции применяется для анализа ее поведения при ударном нагружении. В этом случае используются результаты модального анализа, и для динамической нагрузки с известным спектром определяются максимальные значения перемещений и напряжений в конструкции на каждой из ее собственных частот. Типичным приложением спектрального анализа является расчет на сейсмическое воздействие, который проводится для изучения влияния землетрясений на такие сооружения, как сети трубопроводов, башни и мосты.
Результатом спектрального анализа являются функции отклика, зависящие от частоты. Можно получить четыре различных типа функций отклика: для перемещений, скоростей, ускорений и сил. Пользователь может указать одну из функций отклика (или серию при разной степени демпфирования) в ряде точек модели - это будет однофакторный анализ, а может получить несколько типов функций отклика в разных точках, т.е. провести многофакторный анализ. Спектры отклика можно использовать как для кинематического возбуждения системы, так и для силового.
При выполнении спектрального анализа программа определяет перемещения в конструкции для каждой формы колебаний. Суммарный отклик затем может быть получен с помощью следующих методов: Wilson-CQC, Десять процентов, Двойная сумма, Корень квадратный из суммы квадратов или методом, выбранным пользователем.
Отклик на случайную вибрацию
Анализ случайных колебаний является вариантом спектрального анализа, который применяется для выявления отклика системы на возмущающие силы, не являющиеся детерминированными функциями времени; примерами таких сил могут служить нагрузки, возникающие при работе реактивных или ракетных двигателей.
Процедура определения отклика на случайные колебания подобна спектральному анализу в том, что для его получения требуется выполнить модальный анализ. Отличие, однако, состоит в использовании кривой зависимости спектральной плотности процесса от частоты, которая является статистической характеристикой энергии случайных возмущающих сил. Спектральная плотность может быть выражена через перемещения, скорости, ускорения, давления или усилия. Пользователь имеет возможность либо задать одну из разновидностей спектра и выполнить анализ для различных точек расчетной модели (однофакторный анализ), либо использовать несколько разных спектров плотности энергии и выполнить многофакторный анализ. Можно использовать как кинематическое возбуждение системы, так и силовое.
Предполагается нормальное распределение (распределение Гаусса) спектральной плотности; отклики системы, вычисленные с помощью программы ANSYS, также распределены по нормальному закону. Таким образом, имеется возможность вычислить вероятность, с какой фактический отклик будет превосходить расчетный.
Независимо от используемого типа спектральной плотности процесса в распоряжении пользователя имеются три варианта решения: для перемещений (смещения, напряжения, деформации и усилия), для скоростей (скорости смещений, напряжений, усилий и т.д.) и для ускорений (ускорения смещений, напряжений, усилий и т.д.). Для данного анализа может быть получено любое число этих решений.
Анализ случайных колебаний особенно полезен в аэрокосмической промышленности, где узлы и детали конструкций должны конструироваться так, чтобы выдерживать трудные условия полета. Например, данные об ускорениях, которые испытывает ракета в полете, можно преобразовать к спектральной плотности нагрузок, а затем использовать эти данные для определения отклика узлов ракеты на случайную вибрацию.
ПРОЧНОСТНОЙ ДИНАМИЧЕСКИЙ АНАЛИЗ
Прочностной динамический анализ используется для определения действия на конструкцию или ее составные части нагрузок, зависящих от времени. В отличие от статических расчетов в этом типе анализа принимается во внимание рассеяние энергии и инерционные эффекты переменных во времени нагрузок. Примерами таких нагрузок являются:
- циклические нагрузки (вращающиеся части оборудования);
- внезапно прикладываемые нагрузки (удар или взрыв);
- случайные нагрузки (землетрясение);
- любые другие переменные нагрузки, типа движущихся нагрузок на мосты.
В программе ANSYS все виды динамического анализа основываются на следующем общем уравнении движения в конечно-элементной форме:
[M] {u''} + [C] {u'} + [K] {u} = {F(t)}, [1]
где [M] – матрица масс;
[C] – матрица сопротивлений;
[K] – матрица жесткостей;
{u''} – вектор узловых ускорений;
{u'} – вектор узловых скоростей;
{u} – вектор узловых перемещений;
{F} – вектор нагрузок;
(t) – время.
С помощью этого уравнения определяются значения неизвестных {u}, которые в любой момент времени удовлетворяют условиям равновесия системы при наличии сил инерции и рассеяния энергии.
Программа ANSYS способна выполнять следующие виды динамических расчетов: динамика переходных процессов, модальный анализ, отклик на гармоническое воздействие, спектральный анализ и отклик на случайную вибрацию.
Стационарная теплопроводность
Стационарный тепловой анализ определяет установившееся распределение температур в конструкции и кондуктивные тепловые потоки. Можно задавать такие “нагрузки”, как конвективная теплоотдача с поверхности, тепловые потоки, плотность тепловых потоков, мощность тепловых источников и заданные температуры. Анализ может быть линейным или нелинейным.
В линейном установившемся процессе теплопередачи отсутствует влияние “тепловых” масс (удельных теплоемкостей) и не учитывается зависимость теплофизических свойств материала от температуры. Производная температуры по времени {T} равна нулю, а коэффициенты матрицы эффективной теплопроводности постоянны. В этом случае разрешающее уравнение приводится к виду:
[K] {T} = {Q}.
Эта система линейных совместных уравнений решается за одну итерацию, применяется для расчета процессов кондуктивного и линейного конвективного переноса тепла.
В нелинейном стационарном анализе теплопередачи не рассматриваются эффекты, зависящие от времени (отсутствуют “тепловые” массы). Однако теплофизические свойства материалов (включая и коэффициент конвективной теплоотдачи с поверхности) могут меняться с температурой; кроме того, может иметь место лучистый теплообмен.
Механизм радиационного теплообмена описывается тремя различными способами. Для моделирования переноса тепла излучением между двумя точками пространства используется линейный радиационный конечный элемент. Для описания радиационного теплообмена между поверхностью и точкой используется конечный элемент поверхностного излучения. При решении задач, относящихся к нескольким поглощающим и излучающим поверхностям, используется матричный генератор. В последнем случае имеется возможность учесть полное или частичное перекрытие поверхностей, также как и задать узел в пространстве, который поглощает или излучает энергию. В общем случае переноса тепла излучением плотность радиационного теплового потока {Q}является функцией скорее T4, чем T, т.е. характер процесса явно нелинейный.
В нелинейном анализе матрица теплопроводности является функцией температуры, и решение задачи достигается применением итераций. В программе ANSYS итеративная процедура имеет своей основой метод Ньютона-Рафсона, который предполагает решение последовательности линейных задач для получения нелинейного приближения. Таким образом, уравнение для нелинейной стационарной задачи теплопроводности имеет вид
[K]i
{DT}i+1 = {QA} – {QNR}i ,
где i - номер итерации.
Это уравнение на первой итерации решается при некоторой начальной температуре (которая может быть задана пользователем); в последующих итерациях для вычисления коэффициентов матрицы теплопроводности используются значения температур, полученные на предыдущей итерации. Процесс итераций продолжается, пока не достигается сходимость решения, т.е. пока не будет выполнен установленный пользователем критерий сходимости. Сходимость контролируется по величине невязки вектора нагрузок (потока тепла) и/или по изменению температуры от итерации к итерации.
Результаты решения, для линейного и нелинейного анализа, представляют собой значения температуры и плотности теплового потока в узлах. Эти данные могут быть использованы при постпроцессорной обработке для построения картины изотерм в расчетной модели. Средства постпроцессора можно использовать для получения такой специфической информации, как значения температурных градиентов или потоков в узлах и в центре элемента, а также плотность теплового потока через поверхности излучения (поглощения). Информация выводится в табличной или графической форме.
Нестационарный процесс
Нестационарный тепловой анализ используется для получения распределения температуры в конструкции как функции времени и для определения тепловых потоков при передаче и аккумулировании тепла в системе. Нестационарная теплопроводность имеет дело с линейными и нелинейными задачами. Виды тепловых нагрузок и учитываемых нелинейностей такие же, как и в случае стационарной теплопроводности. Для расчета аккумулируемого в системе тепла используется удельная теплоемкость, которая вводится как свойство материала.
Для решения нестационарной задачи разрешающее уравнение
[C] {T'} + [K] {T} = {Q},
содержащее слагаемое, ответственное за аккумулирование тепла, следует проинтегрировать по времени.
После получения решения можно использовать стадию постпроцессорной обработки для построения картины распределения температур и вывода в табличной или графической форме различной информации (температурные градиенты, плотности теплового потока и т.п.) для любого момента времени нестационарного процесса. Кроме того, для выбранных точек модели можно получить графики зависимости температуры от времени и другие выходные данные.
ТЕПЛОВОЙ АНАЛИЗ
В программе ANSYS реализованы расчетные средства для трех видов теплообмена: кондуктивного, конвективного (свободного и вынужденного) и радиационного. Эти средства используются при проведении стационарного, нестационарного, линейного или нелинейного теплового анализа.
Для конечно-элементного представления системы разрешающее уравнение процесса теплопередачи имеет вид:
[C] {T'} + [K] {T} = {Q},
где [C] – матрица удельных теплоемкостей;
{T'} – производная по времени температуры в узле;
[K] – матрица эффективной теплопроводности;
{T} – вектор узловых температур;
{Q} – вектор эффективного теплового потока в узле.
С помощью программы ANSYS будет выполняться тепловой анализ для следующих задач:
стационарная теплопроводность;
неустановившийся температурный режим;
расчет температурных напряжений и деформаций.
ТЕРМО-ПРОЧНОСТНОЙ АНАЛИЗ
Средства термо-прочностного анализа программы ANSYS позволяют использовать результаты решения задачи теплообмена для проведения прочностного анализа. Такая возможность удобна при определении влияния температурного поля на прочность конструкции. Пользователь может задать тепловую нагрузку отдельно или в совокупности с механическими нагрузками.
В программе ANSYS доступны два способа связывания теплового и прочностного анализов. Первый состоит в том, что эти два анализа делаются друг за другом. Сначала получают температурное поле в модели для заданных граничных условий теплообмена. Значения температур затем используются в виде нагрузок на стадиях препроцессорной подготовки и получения решения при последующем прочностном анализе.
Второй способ предусматривает проведение совместного термо-прочностного решения. В программе ANSYS это достигается использованием конечных элементов связанной задачи, которые имеют как тепловые, так и прочностные степени свободы. Из этих элементов создается расчетная модель и задаются тепловые и механические граничные условия. На каждой итерации выполняется решение тепловой и прочностной задач с использованием значений температур и перемещений, полученных на предыдущей итерации. Имеется возможность вводить в расчетную модель контактные элементы общего типа. Эти элементы допускают теплопередачу через поверхность контакта. Как только контактные поверхности смыкаются, становится возможным процесс теплообмена.
С помощью процедуры совместного решения возможно объединить такие сложные задачи теплообмена и расчета на прочность, как нестационарный тепловой и нелинейный динамический анализы. Например, такой подход можно использовать для анализа биметаллической полосы, которая при нагревании испытывает деформации как тепловой, так и механической природы. В этом случае из-за различия температурных коэффициентов расширения двух металлов возможно появление больших геометрических деформаций, что может сказаться на величине коэффициентов матрицы теплопроводности.
Лабораторная работа №8
НЕСТАЦИОНАРНЫЙ ТЕПЛОВОЙ РЕЖИМ
Цель работы: проанализировать воздействие двух точечных источников 1 и 2 тепла на пластину, приведенную на рисунке 33.
|
Тип анализа |
Нестационарный тепловой анализ конструкции |
|
Тип используемого конечного элемента |
Двумерный твердотельный (Solid) |
|
Тип граничных условий |
Конвекция, точечные нелинейные источники тепла |
|
Возможности |
Нелинейная конвекция и тепловой источник |
Рис. 33
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES… => THERMAL => ОК.
2. Выбираем тип используемого элемента, задаём его толщину и определяемся со свойствами материала:
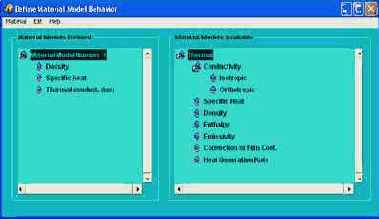



2. Двойным нажатием раскрываем SPECIFIC HEAT и присваиваем C значение 30.
3. Аналогично раскрываем DENSITY и в поле DENS задаем 2788.

M.M. => PREPROCESSOR => -MODELING– CREATE=> –AREAS– RECTANGLE => BY DIMENSIONS… и задаем координаты X1, X2 и Y1, Y2 равные 0, 0.3 и 0, 0.15 соответственно. Нажимаем ОК.
4. Определяем точки на поверхности пластины, на которых будут находиться источники тепла: M.M. => PREPROCESSOR => –MODELING– CREATE => KEYPOINTS => HARD PT ON AREA => HARD PT BY COORD => выделяем поверхность на которой будет находится точка => OK=> указываем координаты 0.075, 0.5, 0=> HARD PT BY COORD => выделяем поверхность на которой будет находится точка => OK => указываем координаты 0.225, 0.1, 0.
5. Разбиваем конструкцию на конечные элементы:
А. Сначала задаем размер конечных элементов:
M.M. => PREPROCESSSOR => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE и переменной SIZE присваиваем значение 0.025, нажимаем ОК.
Б. Производим разбиение:
M.M. => PREPROCESSOR => –MESHING– MESH => –AREAS– FREE => PICK ALL.
6. Выбираем тип анализа:
SOLUTION => –ANALYSIS TYPE– NEW ANALYSIS… => TRANSIENT => OK => OK.
7. Задаем температуру окружающей среды и коэффициент теплопроводности:

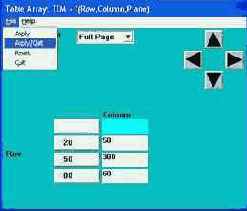
соответственно => OK. В соответствии с рисунком 34 заполняем поля таблицы 1 и потом: FILE => APPLY/QUIT.

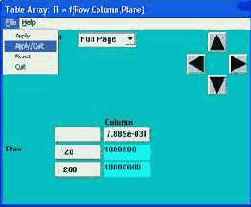
8. Задаем источники температуры в точках, в одной постоянный в другой нет:
M.M. => SOLUTION => –LOADS– APPLY => HEAT GENERAT => ON KEYPOINTS => выделяем точку №5 => OK=> BFK = NEW TABLE => OK=> NAME OF NEW TABLE = IT => I, J, K = 2, 1, 1 соответственно. В соответствии с рисунком 35 заполняем поля таблицы 1 и потом: FILE => APPLY/QUIT. Далее повторяем операцию: M.M. => SOLUTION => –LOADS– APPLY => HEAT GENERAT => ON KEYPOINTS => выделим точку №6 => OK => BFK = CONSTANT VALUE, VALUE = 10E6
=> OK.

9. Определим начальную температуру пластины:
M.M. => SOLUTION=> –LOADS– APPLY => INITIAL CONDIT’N => DEFINE => PICK ALL => LAB = TEMP, VALUE = 20 => OK.

M.M. => SOLUTION => –ANALYSIS TYPE– Sol’s Control => Закладка BASIC => Time at end of loadstep = 10; Number of substeps = 50; Закладка Transient => Ramped Loading => OK.
11. Расчет:

12. Просматриваем результаты расчета:
В районе переменного источника тепла выделяем узел и строим график температуры, выделенного узла, в зависимости от времени при помощи команд:

Выводим поле температур в момент времени, когда температура ранее выделенного узла максимальна при помощи команд:
M.M. => GENERAL POSTPROC => –READ RESULTS– BY TIME/FREQ… и M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => DOF SOLUTION => OK.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с помощью ANSYS при решении нестационарной тепловой задачи, рисунки состояния детали после приложения нагрузок. Выводы.
Лабораторная работа №1
База данных
В программе ANSYS используется одна, центральная, база данных для всего набора сведений, относящихся к модели и результатам решения. Сведения о модели (включая данные о геометрии твердотельной и конечно-элементной моделей, свойствах материалов и т.д.) записываются в базу данных на стадии препроцессорной подготовки. Нагрузки и результаты решения записываются процессором решения. Данные, полученные на основе результатов решения при их постпроцессорной обработке, записываются постпроцессором. Сведения, внесенные одним из процессоров, доступны, при необходимости, для других процессоров. Например, общий постпроцессор может считывать данные, относящиеся к решению и модели, а затем использовать их для постпроцессорных вычислений.
Подмножество программы:
ANSYS/Multiphysics, самый мощный, многоцелевой продукт компании, представляет собой программное средство анализа для широкого круга инженерных дисциплин, которое позволяет проводить расчетные исследования не только в таких отдельных областях знания, как прочность, распространение тепла, механика жидкостей и газов или электромагнетизм, но и решать связанные задачи. Эта программа обеспечивает оптимизацию проектных разработок на уровне, позволяющим моделировать инженерные проблемы в наиболее полной постановке.
ANSYS/Mechanicalä предоставляет широкие возможности для выполнения проектных разработок, анализа и оптимизации: решение сложных задач прочности конструкций, теплопередачи и акустики. Эта программа, обеспечивающая проверку правильности проектных работ, является мощным инструментом для определения перемещений, напряжений, усилий, температур и давлений, а также других важных параметров.
ANSYS/Structuralä выполняет сложный прочностной анализ конструкций с учетом разнообразных нелинейностей, среди которых геометрическая и физическая нелинейности, нелинейное поведение конечных элементов и потеря устойчивости. Используется для точного моделирования поведения больших и сложных расчетных моделей.
ANSYS/LinearPlusä представляет собой более дешевый вариант пакета ANSYS/Mechanical для решения задач линейной статики (с нелинейными элементами зазора и большими прогибами балок и оболочек), динамики и устойчивости.
ANSYS/Thermalä – это самостоятельная, отдельная программа, тоже отпочковавшаяся от пакета ANSYS/Mechanical, для решения тепловых стационарных и нестационарных задач.
ANSYS/PrepPostä является программой, которая обеспечивает быстрое и удобное выполнение полностью параметризованного процесса создания конечно-элементных моделей. Постпроцессор позволяет обрабатывать результаты всех видов анализа, доступных программе ANSYS.
ANSYS/EDä представляет собой программу, обладающую возможностью расчетного кода ANSYS/Multiphysics, но имеющую ограничения по размерам расчетной модели. Этот доступный пакет является идеальным для обучения и подготовки персонала.
Автономные программы:
ANSYS/FLOTRANä – это удобное программное средство для решения разнообразных задач гидродинамики, включая ламинарное и турбулентное течение несжимаемой или сжимаемой жидкости. Эта программа совместно с пакетом ANSYS/Mechanical образует уникальное расчетное средство с оптимизирующими возможностями, которое удовлетворяет самым разнообразным потребностям в области механики и физики.
ANSYS/EMAGä – представляет собой самостоятельный пакет для численного моделирования электромагнитных полей и решения задач, связанных с явлениями электричества и магнетизма. В совокупности с другими пакетами фирмы ANSYS создает многообразные возможности для решения задач механики сооружений с учетом влияния гидродинамических и электромагнитных явлений.
ANSYS/DYNAä – это вариант пакета с решателем явного типа, который предназначен для решения прочностных задач динамики при больших нелинейностях. Эта программа может быть добавлена к уже имеющейся лицензии или использоваться автономно для численного моделирования процессов формования материалов, анализа аварийных столкновений и ударов при конечных деформациях, нелинейном поведении материала и контактном взаимодействии большого числа тел.
Конструкторские пакеты:
ANSYS/ProFEAâ представляет собой программное средство анализа проектных разработок с модернизированными версиями тех возможностей, которые характерны для пакетов фирмы ANSYS, что позволяет вести опережающий анализ и оптимизацию в составе пакета Pro/ENGINEER.
ANSYS/AutoFEAä3D – это безупречно интегрированная программа анализа проектных разработок, функционирующая целиком в среде пакетов AutoCAD версии 13 и Autodesk Mechanical Desktop и позволяющая оценить концептуальную полноту проекта.
Модальный анализ
Модальный анализ используется для определения собственных частот и форм колебаний механических систем. Является важной составной частью всякого динамического анализа, поскольку знание фундаментальных форм и частот колебаний конструкции помогает оценить ее динамическое поведение. Результаты анализа дают возможность установить число форм колебаний и шаг интегрирования по времени, что может обеспечить надежное решение задачи о динамическом поведении системы в неустановившемся режиме. Кроме того, некоторые методы получения решения для переходных процессов нуждаются в результатах модального анализа. С помощью программы ANSYS модальный анализ можно выполнять как для ненагруженной конструкции, так и вслед за нелинейным статическим расчетом.
В программе ANSYS модальный анализ – это решение задачи о свободных (невынужденных), затухающих или незатухающих, колебаниях дискретной системы, которая описывается уравнением [1]. Этому уравнению придается форма, соответствующая задаче о собственных значениях:
( [K] – ?2 [M] ){u}= 0,

Применение модального анализа полезно во всех приложениях, в которых представляет интерес значения собственных частот системы. Например, детали и узлы оборудования следует конструировать так, чтобы избежать их возбуждения на одной из собственных частот в условиях эксплуатации.
Процессоры
Все функции, выполняемые программой ANSYS, объединены в группы, которые называются процессорами. Программа имеет один препроцессор, один процессор решения, два постпроцессора и несколько вспомогательных процессоров, включая оптимизатор. Препроцессор используется для создания конечно-элементной модели и выбора опций для выполнения процесса решения. Процессор решения используется для приложения нагрузок и граничных условий, а затем для определения отклика модели. С помощью постпроцессора пользователь обращается к результатам решения для оценки поведения расчетной модели, а также для проведения дополнительных вычислений, представляющих интерес.
Статический
СТАТИЧЕСКИЙ АНАЛИЗ
Цель работы: построить и выполнить статический расчет уголка с отверстием рис. 2. Уголок закреплен в зоне отверстия и на его левый край приложена сила.
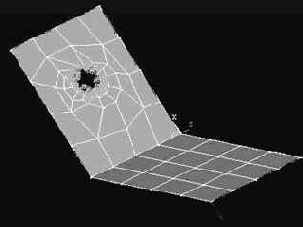
Строим окружность радиусом 0,02 метра:
M.M. => PREPROCESSOR => –MODELING– CREATE => –AREA– CIRCLE
=> SOLID CIRCLE => RADIUS = 0,02 => ОК.
 |
Г. В соответствии с пунктом В перемещаем активную систему координат на центр левой стороны прямоугольника:
U.M. => WORKPLANE => CHANGE ACTIVE CS TO (какую координатную систему сделать активной) => WORKING PLANE, затем U.M. => WORKPLANE => OFFSET WP TO (куда переместить рабочую систему)=> KEYPOINT => выделяем две точки 2 и 3, как показано на рисунке 1=> ОК.
Д. Строим окружность аналогично пункту Б радиусом 0,01 метра.
Е. Складываем полученные фигуры аналогично пункту В.
4. Разбиваем конструкцию на конечные элементы:
M.M. => PREPROCESSOR => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE… => NDIV = 4
=> ОК, затем: M.M. => PREPOCESSOR
=> –MESHING– MESH => –AREAS– FREE+
=> PICK ALL.
5. Проводим модальный анализ не нагруженной конструкции:
M.M. => SOLUTION => NEW ANALYSIS => MODAL (анализ на собственные частоты) => OK, затем: M.M.
=> SOLUTION => ANALISYS OPTIONS => MODOPT = Block Lanczos, No. of modes to extract = 10, MXPAND = Yes, NMODE = 10, ELCALC = No, LUMPM
= No, PSTRES = No => OK => FREQB = 0, FREQE
= 10000
=> ОК.
Выполняем расчет: M.M.
=> SOLUTION => CURRRENT LS => OK.
6. Просматриваем результаты расчета:
 |
=> –CONTOUR PLOT– NODAL SOLU… => PLNSOL = DOF SOLUTION, TRANSLATION USUM
=> OK.
Для просмотра следующих частот, по очереди, второй, третьей и т.д.: M.M. => GENERAL POSTPROC => –READ RESULTS– NEXT SET (следующая частота) N-1 раз, где N – номер собственной частоты, то есть для просмотра третьей частоты нажимаем два раза=> PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU… => PLNSOL
= DOF SOLUTION, TRANSLATION USUM => OK.
7. Проводим анализ преднагруженной конструкции:
A. Нагружаем и закрепляем созданную ранее конструкцию:
M.M. => PREPROCESSOR => LOADS => NEW ANALIS => STATIC
=> OK. Теперь: M.M.
=> PREPROCESSOR => LOADS => ANALYSIS OPTIONS… => NGEOM
= Off; NROPT = Program chosen, ON if necessary; LUMPM
= Yes; пропущенные в описании пункты окна остаются без изменений; PIVCHECK = On => OK.
B. Закрепляем деталь и прикладываем к ней внешнее воздействие:
M.M. => PREPROCESSOR => LOADS => –LOADS– APPLY => DISPLACEMENT => ON LINES => нажимаем на линии закрепления указанные в задании по очереди => ОК
=> ALL DOF => ОК; M.M. => PREPROCESSOR => LOADS => –LOADS– APPLY => FORCE / MOMENT => ON NODES+ (в узле) => нажимаем на указанное заданием место приложения нагрузки => OK
=> LAB = FZ, CONSTANT VALUE; VALUE =–1000 => OK.
Г. Проводим статический расчет преднагруженной конструкции:
M.M. => SOLUTION => CURRRENT LS => OK.
Д. Проводим модальный анализ преднагруженной конструкции:
M.M. => SOLUTION => NEW ANALIS => MODAL => OK. Теперь: M.M.
=> SOLUTION => ANALISYS OPTIONS… => все настройки остаются без изменений по отношению к предыдущему модальному анализу кроме LUMPM = Yes, PSTRES = Yes => ОК => FREQB = 0, FREQE = 10000 => ОК. Затем: M.M. => SOLUTION => CURRRENT LS
=> OK.
Е. Сравниваем результаты расчета преднагруженной конструкции (аналогично пункту 6) и сравниваем с полученными ранее.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с помощью ANSYS при проведении модального анализа, рисунки состояния детали после приложения нагрузок. Сравнение полученных результатов расчета ненагруженной детали с преднагруженной деталью. Выводы.
Лабораторная работа №3
ГАРМОНИЧЕСКАЯ ВИБРАЦИЯ

|
Тип анализа |
Структурный
Рис. 6
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES…=> STRUCTURAL=> ОК.
1. Выполняем следующую последовательность действий:
M.M. => PREFERENCES… => STRUCTURAL => OK. Таким образом, фильтруется все меню под структурный расчет.
2. Задаем свойства материалов и определяемся с типом элементов.
Выбираем тип элементов:
=> ELEMENT TYPE => ADD/EDIT/DELETE => ADD…=> STRUCTURAL SHELL ELASTUC 4 NODE 63 => OK
=> CLOSE. Сначала определяем толщины используемых пластин, для этого: M.M. => PREPROCESSOR => REAL CONSTANTS => ADD/EDIT/DELETE => ADD => ОК и в пункте SHELL THICKNESS AT NODE I TK(I) задаем толщину пластины равную 0,006 метрам
и повторяем операцию ADD
=> ОК, задаем толщину второго материала равную 0,012 метрам. Далее задаём свойства материалов:
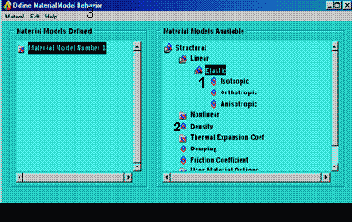
M.M. => PREPROCESSSOR => MATERIAL PROPS => MATERIAL MODELS. Затем, следуя цифрам на рис. 7, выполняем следующие действия:
А. Двойным нажатием мыши на указанные папки выполняем:
STRUCTURAL => LINEAR => ELASTIC => ISOTROPIC. В окне LINEAR ISOTROPIC PROPERTIES FOR MATERIAL NUMBER 1 задаем: модуль Юнга EX = 2е11 Па и коэффициент Пуассона PRXY = 0,27.
Б. Аналогично раскройте DENSITY и в поле плотность DENS задайте 7800 кг/м3.

= 1E+11 Па; PRXY = 0.23; DENS = 2700 кг/м3.
3. Строим деталь:
А. M.M.
=> PREPROCESSOR => MODELING –CREATE– => –AREAS– RECTANGLE => BY DIMENSIONS…, вводим координаты углов: X1 = -0.5, X2
= 0.5, Y1 = 0, Y2
= 1, нажимаем APPLY;
Б. Вводим координаты углов: X1 = -0.3, X2 = 0.3, Y1 = 0, Y2
= 0.5;
В. Для построения третьего прямоугольника повернем систему координат на угол равный 120° (рис. 9):
U.M. => WORK PLANE => OFFSET WP BY INCREMENTS…:
· угол поворота устанавливаем равным 90° и нажимаем на кнопку поворота оси Х против часовой стрелки;
· угол поворота устанавливаем равным 30° и нажимаем на кнопку поворота оси Х против часовой стрелки.
Теперь определяем координаты углов последнего прямоугольника:

=> MODELING –CREATE– => –AREAS– RECTANGLE
=> BY DIMENSIONS… - X1 = -0.3, X2
= 0.3, Y1 = 0, Y2 = 0.5.
4. Соединяем в одно целое все полученные ранее прямоугольники, для этого:
M.M. => PREPROCESSOR =>–MODELING– OPERATE
=> –BOOLEANS– PARTITION => AREAS. Выделяем курсором сначала второй прямоугольник (рис. 8), затем первый и нажимаем ОК. Теперь склеиваем все пластины: M.M.
=> PREPROCESSOR => –MODELING– OPERATE
=> –BOOLEANS– GLUE => AREAS => PICK ALL. Таким образом, мы получаем единую конструкцию.
5. Назначаем каждому прямоугольнику свой материал:
M.M. => PREPROCESSOR =>–ATTRIBUTES– DEFINE => ALL AREAS…
PICKED AREAS+; нажимаем на первый прямоугольник (рис. 8) и нажмите ОК, в появившемся окне выставляем: MAT
= 1, REAL = 1, TYPE
= 1 SHELL63, ESYS = 0 и нажимаем ОК, затем нажимаем ALL AREAS…
PICKED AREAS+, потом нажимаем на второй и третий прямоугольники по очереди, нажимаем OK, затем в окне AREA ATTRIBUTES
выставляем: MAT = 2, REAL = 2, TYPE
= 1 SHELL63, ESYS = 0.
6. Разбиваем конструкцию на конечные элементы:
M.M. => PREPROCESSOR => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE…., переменной SIZE присваиваем значение 0.1, потом нажимаем ОК, затем:
M.M. => PREPROCESSOR => –MESHING– MESH
=> –AREAS– FREE+ => PICK ALL.
7. Проводим расчет гармонической вибрации:
А. Назначаем тип анализа – гармонический: M.M. => SOLUTION => ANALYSIS TYPE– NEW ANALISIS… => HARMONIC.
Б. Закрепляем конструкцию, как показано на рисунке 9 под цифрой 1: MM=>SOLUTION=>APPLY=>DISPLACEMENT=> LINES… и выбираем закрепляемую линию, нажимаем ОК и в появившемся окне выбираем ALL DOF, то есть по всем осям перемещения равны нулю, и нажимаем ОК.
В. Нагружаем конструкцию, как показано на рис. 9 под цифрой 2:
M.M. => SOLUTION => APPLY => PRESSURE
=> ON AREAS, выделяем указанную поверхность, нажимаем ОК, и в окне переменной VALUE задаем значение распределенной нагрузки равное 1000 Н/м2.

M.M. => SOLUTION => –LOAD STEP OPTS– TIME/FREQUENC
=> FREQ AND SUBSTPS… и выставляем значения: HARFRQ = 4…12 – интервал частот, а NSUBST = 50 – количество шагов, STEPPED. Нажимаем ОК. Затем нажимаем MAIN MENU => SOLUTION => CURRRENT LS
=> OK.
6. Просматриваем результаты расчета:
А. Выбираем последовательно три узла, для которых строим графики перемещений и ускорений в зависимости от частоты нагрузки:
M.M.
=> TIMEHIST POSTPRO => DEFINE VARIABLES …, то есть, определяем узлы, с которых будут считываться значения перемещений. Нажимаем на кнопку ADD… и выбираем NODAL DOF RESULT, нажимаем ОК. Выбираем последовательно три узла, рис. 10, подтверждаем выбор нажатием ОК. В появившемся окне выставляем: NVAR (номер переменной) равный 2, 3 и 4 DATA ITEM
равный DOF SOLUTION и TRANSLATION UY, UZ и UZ (все результаты по оси Y и Z) соответственно, нажимаем ОК
потом CLOSE.

M.M.
=> TIMEHIST POSTPRO => GRAPH VARIABLES… и в окне наберем: NVAR1 присвоим значение 2, NVAR2 присваиваем значение 3, NVAR3 присваиваем значение 4; и нажимаем ОК. В результате этого получаем график значений перемещений в зависимости от частот в определенных ранее узлах. Первый резонанс (всплеск значений перемещений) наблюдается для частоты равной 5,28 Гц.
В. Получаем, резонансную частоту равную 5,28 Гц, смотрим форму колебаний конструкции при данной частоте:
M.M.
=> GENERAL POSTPROC => –READ RESULTS– BY TIME/FREQ…, в появившемся окне выставляем все как изображено на рис. 11 и нажимаем ОК.
После этого: M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU… и в появившемся окне переменной PLNSOL присваиваем значения STRESS,
VON MISSES и потом ОК; а если в последнем окне переменной PLNSOL
присваиваем значения DOF COLUTION, TRANSLATION USUM, получаем перемещения конструкции на резонансной частоте.
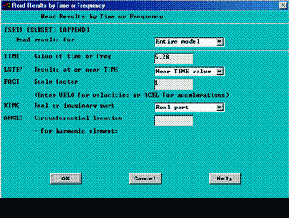
M.M.
=> TIMEHIST POSTPRO => MATH OPERATIONS => Multiply…, в появившемся окне выставляем: IR>5 – номер переменной в которой будет храниться результат перемножения – ускорение, IA>2 – номер переменной в которой хранятся значения перемещений, IB>IC>1
– номер в которой хранятся значения частот ранее заданного интервала, > ОК. Далее выполняем визуализацию графика:
M.M.
=> TIMEHIST POSTPRO => GRAPH VARIABLES… и в появившемся окне переменной NVAR1 присваиваем значение 5, > ОК, получаем график ускорений в выбранном узле для заданного ранее диапазона частот.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с помощью ANSYS при расчете гармонической вибрации, рисунки воздействия вибрации на деталь с параметрами перемещения и ускорения на заданном интервале частот, форма колебаний на резонансной частоте. Выводы.
Лабораторная работа №4.
случайнАЯ вибрациЯ
Цель работы: провести анализ конструкции изображенной на рис. 12 на случайную вибрацию. Деталь закреплена с торцов.
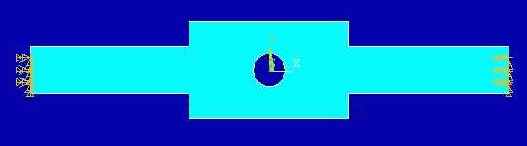
Рис. 12
|
Тип анализа |
Задаем материал:
=> MATERIAL PROPS => MATERIAL MODELS. Затем, следуя цифрам на рисунке 21, выполняем действия:
1)
| 1 |
и в полях TEMPERATURES
задайте: 20, 40, 60, 100; в полях KXX задайте 30, 35, 55, 95.
2) Аналогично раскрываем DENSITY и в поле DENS задаем 7800 кг/м3.
3. Строим деталь (рис. 25):
А. Прямоугольник со сторонами 0.5
и 0.75 метра:
=> –MODELING– CREATE => –AREAS– RECTANGLE
=> BY DIMENSIONS… и задаем координаты X1, X2 и Y1, Y2 равные 0, 0.5 и 0, 0.75
соответственно. Нажимаем ОК.
Б. Окружность радиусом 0.1
метра, с координатами центра окружности 0.25, 0.15 по оси OX и OY:
M. M. => PREFERENCES
=> –MODELING– CREATE => –AREAS– CIRCLE => SOLID CIRCLE далее задаем указанные координаты и радиус и нажимаем ОК.
В. Окружность радиусом 0.1 метра, с координатами центра окружности 0.25, 0.6 по оси OX и OY:
M. M.
=> PREFERENCES => –MODELING– CREATE => –AREAS– CIRCLE => SOLID CIRCLE далее задаем указанные координаты и радиус и нажимаем ОК.
4. Создаем конструкцию посредством логического вычитания геометрических объектов (рис. 25):
M. M.
=> PREFERENCES => –MODELING– OPERATE => –BOOLEANS– SUBTRACT => AREAS, затем нажимаем на прямоугольник 1 и на ОК, далее нажимаем сначала на окружность 2, потом 3, потом ОК.
5. Разбиваем конструкцию на конечные элементы рис. 26:

M. M. => PREFERENCES => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE и переменной SIZE присваиваем значение 0.025, нажимаем ОК.
Б. Проводим разбиение:
M.M. => PREFERENCES => –MESHING– MESH => –AREAS– FREE
=> PICK ALL.
5. Задаем граничные условия рис. 26:
А. Задаем температуру окружающей среды, контактирующую с линией 1: M.M. => SOLUTION => –LOADS– APPLY => CONVECTION => ON LINES и нажимаем на данную линию, потом ОК. В окне, переменной VALI
и VAL2I присваиваем значение 20 и нажимаем ОК.
Б. Задаем температуру, действующую на линию 2:
M.M. => SOLUTION=> –LOADS– APPLY
=> CONVECTION => ON LINES и нажимаем на данную линию, потом ОК. В окне, переменной VALI и VAL2I присваиваем значение 110 и нажимаем ОК.
В. Определяем величину шага:
M.M. => SOLUTION => –LOAD STEP OPTS– TIME/FREQUENC => TIME AND SUBSTPS
и в окне задаем переменным TIME
и NSUBST значение 1 и нажимаем ОК.
6. Проводим расчет:

=> –SOLVE– CURRENT LS
=> OK.
7. Просматриваем результаты:
А. Картины распределения температуры:
M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => DOF SOLUTION => OK.
Б. График температуры на заданном пути:
a) Задаем путь, например:
M.M. => GENERAL POSTPROC
=> PLOT RESULTS=> PATH OPERATIONS=> DEFINE PATH => BY NODES выделяем два узла на противоположных сторонах конструкции (рис. 27), где 1 – начало пути и 2 – его конец, и нажимаем ОК, переменной NAME
присваиваем имя, например TEMP, и нажимаем ОК.
б) Определяем, что выводить на графике:
M.M.
=> GENERAL POSTPROC => PLOT RESULTS => PATH OPERATIONS => MAP ONTO PATH…, где выбираем PDEF значение DOF SOLUTION и переменной /PBC
устанавливаем галочку YES и нажимаем ОК.
в) Вводим в M.M. => GENERAL POSTPROC => PLOT RESULTS => PATH OPERATIONS
=> –PLOT PATH ITEM– ON GRAPH выбираем заданное имя пути TEMP и нажимаем ОК, в результате выводим график изображенный на рисунке 28.
В. График величины теплового потока по заданному пути:
a) Определяем, что выводить на графике:
M.M. => GENERAL POSTPROC => PLOT RESULTS => PATH OPERATIONS
=> MAP ONTO PATH…, где выбираем PDEF значение FLUX & GRADIENT, THERMAL FLUX TFSUM и нажимаем ОК.
b)
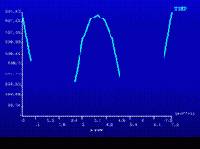
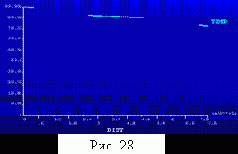
=>PATH OPERATIONS =>– PLOT PATH ITEM– ON GRAPH выбираем TFSUM и нажимаем, ОК. В результате получаем график представленный на рисунке 29.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с
помощью ANSYS при проведении теплового анализа, рисунки состояния детали после приложения нагрузок. Выводы.
Структурный, случайная вибрация
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES… => STRUCTURAL => ОК.
Тип элементов M.M. => PREPROCESSSOR => ELEMENT TYPE => ADD/EDIT/DELETE => ADD… => STRUCTURAL SHELL ELASTUC 4 NODE 63 => OK => CLOSE.
Определяем толщину M.M => PREPROCESSOR => REAL CONSTANTS => ADD/EDIT/ DELETE => ADD => ОК и в пункте SHELL THICKNESS AT NODE I TK(I) задаем толщину пластины равную 0.0007 метрам. Задаем свойства материала:
M.M. => PREPROCESSSOR => MATERIAL PROPS => MATERIAL MODELS. Затем, следуя цифрам на рисунке 13, выполняем действия:
А. Двойным нажатием мыши на указанные папки выполняем: STRUCTURAL => LINEAR => ELASTIC => ISOTROPIC. В окне LINEAR ISOTROPIC PROPERTIES FOR MATERIAL NUMBER 1 задаем: модуль Юнга EX = 2е11 Па и коэффициент Пуассона PRXY = 0.27.
Б. Аналогично раскрываем DENSITY и в поле плотность DENS задаем 7800 кг/м3.
3. Строим деталь, следуя цифрам (рисунок 14):

APPLY;
Б. Вводим координаты углов – X1 = 0.05, X2 = 0.15, Y1 = -0.015, Y2 = 0.015, нажмите APPLY;
В. Вводим координаты углов - X1= -0.05, X2= -0.15, Y1= -0.015, Y2= 0.015, нажимаем ОК;
Г. Складываем полученные фигуры:
M.M. => PREPROCESSOR => –MODELING– OPERATE => –BOOLEANS– ADD => AREAS => PICK ALL;
Д. Строим окружность:
M.M. => PREPROCESSOR => MODELING –CREATE– => –AREAS– CIRCLE => SOLID CIRCLE => RADIUS = 0.01 => OK;
Е. Вычитаем из полученной фигуры построенную окружность:
MM => PREPROCESSOR => –MODELING– OPERATE => –BOOLEANS– SUBTRACT => AREAS => выделяем фигуру, из которой будет производится вычитание => OK => выделяем вычитаемый объект => OK.
4. Разбиваем конструкцию на конечные элементы:
Разбиваем конструкцию на конечные элементы:
M.M. => PREPROCESSOR => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE…, переменной SIZE присваиваем значение 0.01, потом нажимаем ОК, затем: M.M. => PREPROCESSOR => –MESHING– MESH => –AREAS– FREE+ => PICK ALL.
5. Задаем граничные условия и производим расчет:
А. Выбираем модальный анализ:
MM => SOLUTION => NEW ANALISIS… => MODAL, затем: M.M. => SOLUTION => ANALISYS OPTIONS => MODOPT = Block Lanczos, No. of modes to extract = 10, MXPAND = Yes, NMODE = 10, ELCALC = Yes, LUMPM = No, PSTRES = No => OK => FREQB = 0, FREQE = 10000 => ОК.
Б. Закрепляем конструкцию, как показано на рисунке 14 под буквами A и B:
MM => SOLUTION => APPLY => DISPLACEMENT => LINES… и выбираем закрепляемые линии, нажимаем ОК и в появившемся окне выбираем ALL DOF, то есть по всем осям перемещения равны нулю, и нажимаем ОК.
6. Проводим расчет:
M.M. => SOLUTION => CURRRENT LS => OK.
7. Нажимаем M.M.=> FINISH, для выгрузки из задействованной ANSYS памяти предыдущих операций.
8. Проводим спектральный анализ:
M.M. => SOLUTION => NEW ANALYSIS => SPECTRUM, затем выбираем:
M.M. => SOLUTION => ANALYSIS OPTIONS => SPOPT = P.S.D., NMODE = 10, ELCALC = Yes => OK.
9. M.M. => SOLUTION => APPLY => SPECTRUM => –BASE PSD EXCIT– NODES => нажимаем радио-кнопку BOX и выделяем узлы сначала с одного торца потом с другого как показано на рисунке 35 (обведены красными прямоугольниками) => LAB = NODAL Z => OK.
10. M.M. => SOLUTION => SPECTRUM => – PSD– SETTINGS => PSDUNIT = ACCEL(g**2/Hz), GVALUE = 9.8
=> OK.
11. M.M. => SOLUTION => SPECTRUM => –PSD– PSD vs FREQ => OK => в появившуюся таблицу занесите: в первый столбец – полученные собственные частоты, во второй – следующие значения: => OK.
|
Frequency |
PSD value |
Frequency |
PSD value |
Frequency |
PSD value |
Frequency |
PSD value |
Frequency |
PSD value |
|
30 |
0.002 |
46 |
0.0025 |
201 |
0.004 |
301 |
0.006 |
401 |
0.065 |
|
45 |
0.002 |
200 |
0.0025 |
300 |
0.004 |
400 |
0.006 |
850 |
0.008 |
12. M.M. => SOLUTION => SPECTRUM => –PSD– CALCULATE PF => OK.
13. M.M. => SOLUTION => SPECTRUM => –PSD– CALC CONTROLS => DISP = Relative to base, VELO =
Relative to base,
ACEL = Relative to base => OK.
14. M.M. => SOLUTION => SPECTRUM=> –PSD– MODE COMBINE => OK.
15. Проводим расчет:
M.M. => SOLUTION => CURRRENT LS => OK.
16. Просматриваем результаты расчета:
А. Для вывода перемещения и напряжения необходимо: в командной строке ANSYS INPUT набираем команду SET, 3, 1 после чего уже можно визуализировать выходные данные посредством команд:
M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => DOF SOLUTION TRANSLATION USUM => OK – поле перемещений.
M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => STRESS VON MISES => OK – поле напряжений по Мизесу.
Для просмотра скоростей и ускорений воспользуемся командами SET,4,1 и SET,5,1 соответственно, в той же командной строке, и уже потом для визуализации введем функцию M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => DOF SOLUTION TRANSLATION USUM => OK.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с помощью ANSYS случайной вибрации, рисунки состояния детали после приложения нагрузок. Выводы.
Лабораторная работа №5
ДИНАМИЧЕСКОЕ ВОЗДЕЙСТВИЕ (УДАР)
Цель работы: провести анализ конструкции (рис. 15) подвергнутой динамическому воздействию.
 |
|
Тип анализа |
Термоупругий расчет
Цель работы: выполнить связанную тепловую и прочностную задачу для конструкции приведенной на рисунке 30.
| Тип анализа | Связанный тепловой и прочностной расчет для неоднородной конструкции | ||
| Тип используемого конечного элемента | Двумерный твердотельный (Thermal Solid) | ||
| Тип граничных условий | Назначение температуры узлам сетки | ||
| Возможности | Наложение температурного поля в прочностном анализе в качестве нагрузки |
Рис. 30
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES…=> THERMAL => ОК.
2. Выбираем тип используемого элемента, задаём его толщину и определяемся со свойствами материала:
3
2
| 1 |
M.M. => PREPROCESSSOR => MATERIAL PROPS => MATERIAL MODELS. Затем, следуя цифрам на рисунке 31, выполняем действия:
A.
– STRUCTURAL => LINEAR => ELASTIC => ISOTROPIC: EX = 2 E11, PRXY = 0.22 => OK;
– STRUCTURAL => DENSITY: DENS = 7800;
– STRUCTURAL => THERMAL EXPANSION COEF => ISOTROPIC: ALPX = 1E-7.
Б.
– THERMAL=> CONDUCTIVITY => ISOTROPIC: KXX = 30;
– THERMAL=> SPECIFIC HEAT: C = 100.
В. MATERIAL => NEW MODEL: 2 => OK.
Г. Первыми двумя пунктами задаем свойства стали, третьим - определяем второй материал. Повторяем пункт 1 и 2, задаем свойства алюминия с параметрами: EX = 1.69E10, PRXY = 0.25, DENS = 2780, ALPX = 1E-6, KXX = 40, C = 80.
3. Строим деталь:

=> –AREAS– RECTANGLE => BY DIMENSIONS… и задаем координаты X1, X2 и Y1, Y2 равные 0, 0.3 и 0, 0.06
соответственно. Нажимаем ОК.

и d, получим точку f.
В. M.M. => PREFERENCES => –MODELING– CREATE
=> –LINES– LINES => STRAIGHT LINE выделяем точки e потом f и нажимаем ОК, получаем линию.
3. Разделяем полученный прямоугольник по построенной линии:
M.M. => PREFERENCES => –MODELING– OPERATE => DIVIDE=> AREA BY LINE => нажимаем на прямоугольник => OK=> нажимаем на линию => OK.
4. Задаем каждой половине свой материал:
M.M. => PREFERENCES => –ATTRIBUTES– DEFINE => PICKED AREAS => выделяем верхнюю половину => OK => OK => PICKED AREAS => выделяем нижнюю половину => OK => MATERIAL NUMBER = 2 => OK.
5. Разбиваем конструкцию:
А. Сначала задаем средний размер грани конечных элементов:
M.M. => PREFERENCES => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE и переменной SIZE присваиваем значение 0.01, нажимаем ОК.
Б. Производим разбиение:
M.M. => PREFERENCES => –MESHING– MESH => –AREAS– FREE => PICK ALL.
6. Задаем граничные условия для теплового расчета:
А. M.M. => SOLUTION => –LOADS– APPLY =>
–THERMAL– TEMPERATURE => ON LINES => выделяем линию bd (рис. 32) => OK => VALUE = 20 =>OK.
Б. M.M. => SOLUTION => –LOADS– APPLY =>
–THERMAL– TEMPERATURE => ON LINES => выделяем линию ac (рис. 32) => OK=> VALUE = 40 =>OK.
7. Проводим расчет:
M.M. => SOLUTION => –SOLVE– CURRENT LS => OK.
8. Переключаемся на прочностной анализ, используя результаты теплового:
А. M.M. => PREPROCESSOR => ELEMENT TYPE => SWITCH ELEM TYPE => THERMAL TO STRUCTURAL => OK.
Б. M.M. => SOLUTION => –LOADS– APPLY =>
–STRUCTURAL– TEMPERATURE => FROM THERM ANALY => выбираем файл с расширением *.rth, где *– название рабочего файла => OK.
В. Закрепляем конструкцию по линии ab
(рис. 32):
M.M. => SOLUTION => –LOADS– APPLY => –STRUCTURAL– DISPLACEMENT => ON LINES => выделяем линии ae и eb => OK => ALL DOF => OK.
7. Проводим расчет:
M.M. => SOLUTION => –SOLVE– CURRENT LS => OK.
8. Просматриваем результаты расчета:
А. M.M.=> GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => DOF SOLUTION TRANSLATION USUM => OK.
Б. M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => STRESS VON MISES => OK.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с помощью ANSYS при проведении термоупругого расчета, рисунки состояния детали после приложения нагрузок. Выводы.
Лабораторная работа №8
НЕСТАЦИОНАРНЫЙ ТЕПЛОВОЙ РЕЖИМ
Цель работы: проанализировать воздействие двух точечных источников 1 и 2 тепла на пластину, приведенную на рисунке 33.
|
Тип анализа |
Нестационарный тепловой анализ конструкции |
|
Тип используемого конечного элемента |
Двумерный твердотельный (Solid) |
|
Тип граничных условий |
Конвекция, точечные нелинейные источники тепла |
|
Возможности |
Нелинейная конвекция и тепловой источник |
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES… => THERMAL => ОК.
2. Выбираем тип используемого элемента, задаём его толщину и определяемся со свойствами материала:



2. Двойным нажатием раскрываем SPECIFIC HEAT и присваиваем C значение 30.
3. Аналогично раскрываем DENSITY и в поле DENS задаем 2788.

M.M. => PREPROCESSOR => -MODELING– CREATE=> –AREAS– RECTANGLE => BY DIMENSIONS… и задаем координаты X1, X2 и Y1, Y2 равные 0, 0.3 и 0, 0.15 соответственно. Нажимаем ОК.
4. Определяем точки на поверхности пластины, на которых будут находиться источники тепла: M.M. => PREPROCESSOR => –MODELING– CREATE => KEYPOINTS => HARD PT ON AREA => HARD PT BY COORD => выделяем поверхность на которой будет находится точка => OK=> указываем координаты 0.075, 0.5, 0=> HARD PT BY COORD => выделяем поверхность на которой будет находится точка => OK => указываем координаты 0.225, 0.1, 0.
5. Разбиваем конструкцию на конечные элементы:
А. Сначала задаем размер конечных элементов:
M.M. => PREPROCESSSOR => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE и переменной SIZE присваиваем значение 0.025, нажимаем ОК.
Б. Производим разбиение:
M.M. => PREPROCESSOR => –MESHING– MESH => –AREAS– FREE => PICK ALL.
6. Выбираем тип анализа:
SOLUTION => –ANALYSIS TYPE– NEW ANALYSIS… => TRANSIENT => OK => OK.
7. Задаем температуру окружающей среды и коэффициент теплопроводности:

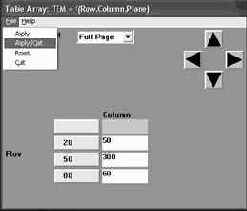
соответственно => OK. В соответствии с рисунком 34 заполняем поля таблицы 1 и потом: FILE => APPLY/QUIT.

8. Задаем источники температуры в точках, в одной постоянный в другой нет:
M.M. => SOLUTION => –LOADS– APPLY => HEAT GENERAT => ON KEYPOINTS => выделяем точку №5 => OK=> BFK = NEW TABLE => OK=> NAME OF NEW TABLE = IT => I, J, K = 2, 1, 1 соответственно. В соответствии с рисунком 35 заполняем поля таблицы 1 и потом: FILE => APPLY/QUIT. Далее повторяем операцию: M.M. => SOLUTION => –LOADS– APPLY => HEAT GENERAT => ON KEYPOINTS => выделим точку №6 => OK => BFK = CONSTANT VALUE, VALUE = 10E6
=> OK.

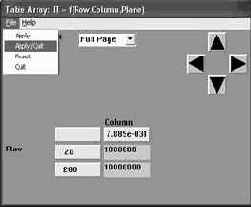
9. Определим начальную температуру пластины:
M.M. => SOLUTION=> –LOADS– APPLY => INITIAL CONDIT’N => DEFINE => PICK ALL => LAB = TEMP, VALUE = 20 => OK.

M.M. => SOLUTION => –ANALYSIS TYPE– Sol’s Control => Закладка BASIC => Time at end of loadstep = 10; Number of substeps = 50; Закладка Transient => Ramped Loading => OK.
11. Расчет:

12. Просматриваем результаты расчета:
В районе переменного источника тепла выделяем узел и строим график температуры, выделенного узла, в зависимости от времени при помощи команд:

Выводим поле температур в момент времени, когда температура ранее выделенного узла максимальна при помощи команд:
M.M. => GENERAL POSTPROC => –READ RESULTS– BY TIME/FREQ… и M.M. => GENERAL POSTPROC => PLOT RESULTS => –CONTOUR PLOT– NODAL SOLU => DOF SOLUTION => OK.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов расчета с помощью ANSYS при решении нестационарной тепловой задачи, рисунки состояния детали после приложения нагрузок. Выводы.
Возможности
Порядок выполнения работы:
1. Задаем рабочее имя:
UTILITI MENU=> FILE=> CHANGE JOBNAME … задаем переменной FILNAM свое значение вместо указанного FILE, при этом изменяется имя проекта (группы файлов).
2. Определяем тип анализа:
MAIN MENU=> PREFERENCES…=> STRUCTURAL=> ОК.
3. Выбираем тип используемого элемента и толщину пластин составляющих конструкцию:
MAIN MENU=> PREPROCESSOR=> ELEMENT TYPE=> ADD/EDIT/DELETE…=> ADD…=> STRUCTURAL
SHELL ELASTUC 4 NODE 63 => ОК=> CLOSE - выбор элемента.
Определяем толщину пластин. Для этого:
M.M.=> PREPROCESSOR => REAL CONSTANTS=> ADD/EDIT/DELETE…=> ADD…=> ОК=> SHELL
THICKNESS AT NODE I TK(I) = 0.003 метра=> ОК=> CLOSE.
4. Выбираем свойства материала и задаем его характеристики.
M.M. => PREPROCESSOR => MATERIAL PROPS => MATERIAL MODELS…=> MATERIAL MODELS AVAILABLE=> STRUCTURAL=>LINEAR=>ELASTIC=> ISOTROPIC=> EX = 2е11 Па, PRXY = 0,3 => ОК=> DENSITY => DENS = 7800 кг/куб.м..
 |
5. Cтроим деталь (Modeling):
A. Первый прямоугольник:
M.M. => PREPROCESSOR=> –MODELING– CREATE => –AREA– RECTANGLE => BY DIMENSIONS… (построение прямоугольника по заданным размерам) => Х1 = 0 м; X2 = 0,05 м; Y1 = 0 м; Y2 = 0,04 м => ОК.
Б. Окружность радиусом 0,005 метра:
M.M. => PREPROCESSOR=> –MODELING– CREATE => –AREA– CIRCLE => SOLID CIRCLE+=> WP X = 0.03; WP Y = 0.02; RADIUS
= 0.005
=> ОК.
B. Отверстие:
Вычитаем из прямоугольника окружность. Для этого, сначала выделяем поверхность, из которой надо вычесть, а потом выделяем вычитаемую поверхность:
M.M.=> PREPROCESSOR => –MODELING– OPERATE => SUBTRACT => AREAS+=> нажимаем прямоугольник за пределами вычитаемой окружности=> APPLY=> нажимаем внутри окружности => ОК.
Г. Второй прямоугольник:
Поворачиваем рабочую систему координат. ANSYS позволяет перемещать и поворачивать рабочую систему координат так, как это угодно пользователю. То есть, чтобы нарисовать вторую пластину, нужно повернуть рабочую плоскость вокруг оси OY по часовой стрелке на 120°.
U.M. => WORK PLANE => OFFSET WP BY INCREMENTS…, появится форма для изменения рабочей плоскости (рис. 3). Прежде чем производить поворот, необходимо выставить угол поворота оси на бегунке (см. рис. 2) равный 90° и нажать кнопку, помеченную на рис. 3 стрелкой, затем выставить на бегунке угол поворота оси равный уже 30° и нажать ту же кнопку. По завершении вращения нажимаем кнопку ОК. В результате этих операций рабочая система координат повернется в нужном направлении на требуемый угол равный 120°. В текущем положении рабочей системы координат строим прямоугольник согласно пункту 5 А.
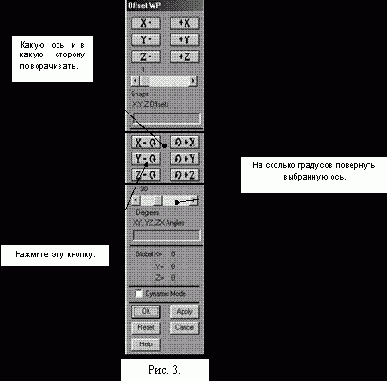
Е. «Склеиваем» геометрические объекты построенной конструкции: M.M. => PREPROCESSOR =>
–MODELING– OPERATE=> GLUE=> AREAS => PICK ALL.
Ж. Для корректного задания нагружения, выставим рабочую систему координат на 120° назад, то есть необходимо выполнить пункт 5 Г с точностью до наоборот. Сохраняем результат работы.
6. Разбиваем конструкцию на конечные элементы:
M.M.=> PREPROCESSOR => -MESHING–
SIZE CNTRLS => -MANUAL SIZE– –GLOBAL– SIZE… => NDIV
= 4 => ОК. Таким образом мы настроили геометрию на разбиение, теперь:
M.M. => PREPROCESSOR => –MESHING– MESH => –AREAS– FREE+=> PICK ALL.
7. Выбираем тип анализа:
M.M. => SOLUTION => –ANALYSIS TYPE– NEW ANALIS… => STATIC
=> ОК.
8. Прикладываем к конструкции внешнее воздействие:
M.M. => SOLUTION => –LOADS– APPLY => –STRUCTURAL– FORCE/MOMENT => ON KEYPOINTS+=> выделяем точку, к которой будет приложена сила, как показано на рис. 2 => ОК=> Lab =FX, Value = –50 Н => ОК.
9. Закрепляем конструкцию:
M.M. => SOLUTION => –LOADS– APPLY => –STRUCTURAL– DISPLACEMENT => ON LINES+ => выделяем окружность (она разбита на четыре сектора, поэтому надо последовательно нажать на каждый из них) => ОК => Lab2 = ALL DOF => ОК. Таким образом, все степени свободы узлов на отверстии равны нулю.
10. Запускаем на решение:
M.M. => SOLUTION => –SOLVE– CURRENT LS => ОК.
11. Просмотриваем поля суммарного вектора перемещений:
M.M. => GENERAL POSTPROC
=> PLOT RESULTS=> –CONTOUR– NODAL SOLU… => Item, Comp
= DOF solution, Translation USUM => OK.
Вывод поля напряжений по Мизесу:
M.M. => GENERAL POSTPROC
=> PLOT RESULTS => –CONTOUR– NODAL SOLU… => Item, Comp
= Stress, von Mises SEQV => OK.
Содержание отчета: краткие теоретические сведения, подробное описание всех шагов статического расчета, рисунки состояния детали после приложения силы (суммарный вектора перемещений и поля напряжения по Мизесу с указанием наиболее нагруженного участка). Выводы.
Лабораторная работа №2
МОДАЛЬНЫЙ АНАЛИЗ
Цель работы: рассчитать собственные частоты конструкции, приведенной на рис. 4, в не нагруженном состоянии; сделать анимационный файл к одной или нескольким (по указаниям преподавателя) собственным частотам; провести анализ собственных частот той же конструкции в преднагруженном состоянии и сравнить результаты.

|
Тип анализа |
и удобная программа. Каждая ее
Введение
Сегодня ANSYS – это чрезвычайно мощная и удобная программа. Каждая ее версия включает новые и расширяет прежние возможности пакета, что делает программу быстродействующей, более гибкой и удобной. Эти ее качества помогают пользователям справиться с непрерывно возрастающими запросами современного промышленного производства.
Программа ANSYS – это гибкое, надежное средство проектирования и анализа. Как новичкам, так и опытным пользователям эта программа предлагает непрерывно растущий перечень расчетных средств, которые могут:
– учесть разнообразные конструктивные нелинейности;
– дать возможность решить самый общий случай контактной задачи для поверхностей;
– допускать наличие больших (конечных) деформаций и углов поворота;
– позволять выполнить интерактивную оптимизацию и анализ влияния электромагнитных полей,
– получaть решение задач гидроаэродинамики и многое другое - вместе с параметрическим моделированием, адаптивным перестроением сетки, использованием р-элементов и обширными возможностями создания макрокоманд с помощью языка параметрического проектирования программы ANSYS (APDL).
Предлагаемое методическое пособие предназначено для изучения студентами основ механических и тепловых процессов на базе системы ANSYS. ANSYS является универсальной конечно-элементной программой, применяемой для решения прочностных, тепловых, акустических, гидро и газодинамических задач. Данное методическое пособие представляет собой теоретический и практический материал по важнейшим разделам моделирования механических и тепловых процессов. Для эффективности и облегчения процесса обучения текст методического пособия иллюстрирован.
В методическом пособии приведены указания по проведению восьми лабораторных работ. Лабораторная работа №1 посвящена основам работы в ANSYS, простейшим геометрическим построениям и решению прочностной статической задачи. В лабораторной работе №2 рассматривается решение задачи на собственные частоты преднагруженной и не преднагруженной конструкции. Лабораторная работа №3 приведено решение задачи на гармоническое воздействие. Расчету конструкции на случайную вибрацию посвящена работа №4. В лабораторной работе №5 рассмотрен расчет конструкции на произвольное динамическое воздействие Лабораторные работы № 6, 8 рассматривают решению тепловых нелинейных стационарных и нестационарных задач. Лабораторная работа №7 рассматривает решение связанной тепловой и прочностной задачи.
