Оценка погрешности алгоритма прямоугольников
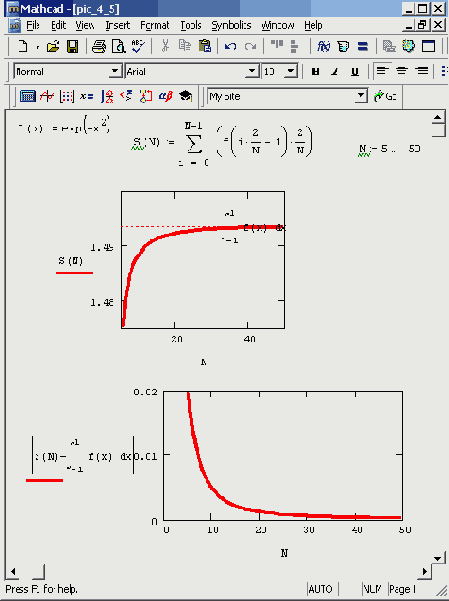
Рисунок 4.5. Оценка погрешности алгоритма прямоугольников
Недостатком перечисленных традиционных алгоритмов являются затруднения в количественной оценке погрешности. Аналитические формулы для погрешности включают, помимо множителя ьк, задающего, собственно, порядок аппроксимации метода, сомножитель, характеризующий величину производной (определенного высшего порядка) подынтегральной функции. Оценить ее значение при конкретных расчетах очень сложно, и поэтому, соответственно, сложно вычислить суммарную погрешность алгоритма. В то же время сведения о величине погрешности являются очень важными, и, чаще всего, желательно иметь их количественную оценку, чтобы оптимально выбрать число разбиений интервала интегрирования N.
Для апостериорной оценки погрешности можно, например, применять анализ зависимости s(N), подсчитанной для нескольких значений N (Рисунок 4.5). Зная, что, с одной стороны, s(N) изменяется по определенному степенному закону N~K, и, с другой, s(N)->i (к точному значению интеграла), можно довольно точно определить погрешность метода. На нижнем графике Рисунок 4.5 приведена зависимость погрешности от N (правда, в данном случае мы использовали для наглядности графика точное значение интеграла, которое в практических случаях, конечно, неизвестно). Именно с подобной процедурой и связан алгоритм расчета определенных интегралов, использованный в Mathcad, который будет представлен в следующем разделе.
