График плохо обусловленной системы двух уравнений
Рисунок 8.10. График плохо обусловленной системы двух уравнений
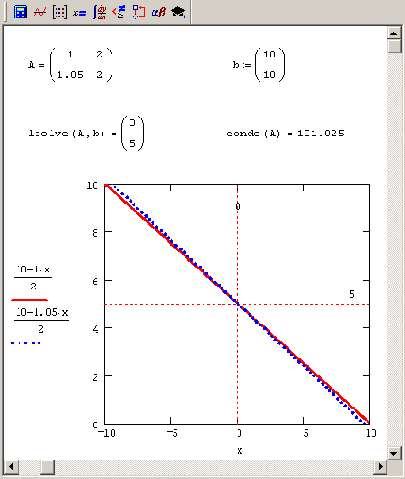
Из Рисунок 8.10 видно, что прямые, соответствующие плохо обусловленной СЛАУ, располагаются в непосредственной близости друг от друга (почти параллельны). В связи с этим малые ошибки в расположении каждой из прямых могут привести к значительным погрешностям локализации точки их пересечения (решения СЛАУ) в противоположность случаю хорошо обусловленной системы, когда малые погрешности в наклоне прямых мало повлияют на место точки их пересечения (Рисунок 8.9).
Примечание 2
Примечание 2
Плохая обусловленность матрицы типична и при реконструкции экспериментальных данных, задаваемых переопределенными (несовместными) СЛАУ (например, в задачах томографии). Именно такой случай приведен в качестве примера в следующем разделе (см. листинг 8.16 ниже).
Метод регуляризации
Для решения некорректных задач, в частности, вырожденных и плохо обусловленных СЛАУ, разработан очень эффективный прием, называемый регуляризацией. В его основе лежит учет дополнительной априорной информации о структуре решения (векторе априорной оценки хо), которая очень часто присутствует в практических случаях. В связи с тем, что регуляризация была подробно рассмотрена в разд. 6.3.3, напомним лишь, что задачу решения СЛАУ Аx=b можно заменить задачей отыскания минимума функционала Тихонова:
?(х,?) = |Ах-b|2+?|х-х0|2. (8.3)
Здесь Я, — малый положительный параметр регуляризации, который необходимо подобрать некоторым оптимальным способом. Можно показать, что задачу минимизации функционала Тихонова можно, в свою очередь, свести к решению другой СЛАУ:
(АTА+?I)-х=АTВ+?х0, (8.4)
которая при ?->0 переходит в исходную плохо обусловленную систему, а при больших x, будучи хорошо обусловленной, имеет решение х0. Очевидно, оптимальным будет некоторое промежуточное значение А, устанавливающее определенный компромисс между приемлемой обусловленностью и близостью к исходной задаче. Отметим, что регуляризационный подход сводит некорректную задачу к условно-корректной (по Тихонову) задаче отыскания решения системы (8.4), которое, в силу линейности задачи, является единственным и устойчивым.
Приведем, без излишних комментариев, регуляризованное решение вырожденной системы, которая была представлена на Рисунок 8.8.
