Решение двух близких плохо обусловленных СЛАУ
Листинг 8.14. Решение двух близких плохо обусловленных СЛАУ
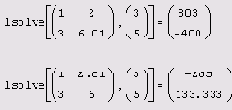
Каждая строка листинга 8.14 содержит решение двух очень близких плохо обусловленных СЛАУ (с одинаковой правой частью ь и мало отличающимися матрицами А). Несмотря на близость, точные решения этих систем оказываются очень далекими друг от друга. Надо заметить, что для системы двух уравнений точное решение получить легко, однако при решении СЛАУ большой размерности незначительные ошибки округления, неминуемо накапливаемые при расчетах (в том числе и "точным" алгоритмом Гаусса), приводят к огромным погрешностям результата. Возникает вопрос: имеет ли смысл искать численное решение, если заранее известно, что, в силу неустойчивости самой задачи, оно может оказаться совершенно неправильным?
Еще одно соображение, которое вынуждает искать специальные методы решения плохо обусловленных СЛАУ (даже приведенной в качестве примера в листинге 8.14 системы двух уравнений), связано с их физической интерпретацией как результатов эксперимента. Если изначально известно, что входные данные получены с некоторой погрешностью, то решать плохо обусловленные системы не имеет вовсе никакого смысла, поскольку малые ошибки модели (матрицы А и вектора ь) приводят к большим ошибкам решения. Задачи, обладающие такими свойствами, называются некорректными.
Чтобы лучше понять причину некорректности, полезно сравнить графическую интерпретацию хорошо (Рисунок 8.9) и плохо (Рисунок 8.10) обусловленной системы двух уравнений. Решение системы визуализируется точкой пересечения двух прямых линий, изображающих каждое из уравнений.