Регуляризация вырожденной СЛАУ
Листинг 8.15.Регуляризация вырожденной СЛАУ
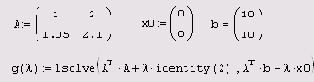
Заключительным шагом регуляризации является выбор оптимального ?. Имеется, по крайней мере, два соображения, исходя из которых, можно выбрать параметр регуляризации, если опираться на зависимость от него невязки. В рассматриваемом примере применим критерий определения ?, опирающийся -на подбор нормы невязки, равной априорной оценке погрешностей задания входных данных: матрицы А и вектора b, т. е. величине |?A| + |5?|. Например, можно выбрать норму невязки и, соответственно, параметр ? и решение х(?), которые отмечены на Рисунок 8.11 и 8.12 пунктирами.
Примечание 3
Примечание 3
Другим вариантом выбора ?, не требующим никаких априорных соображений относительно погрешностей модели, является так называемый квазиоптимальный метод, рассмотренный в разд. 6.3.3.
Примечание 4
Примечание 4
Полезно убедиться в том, что формула (8.4) в случае линейной задачи дает тот же результат, что и общая формула (8.3). Для этого достаточно изменить в листинге 8.15 последнюю строку, выражающую решение СЛАУ (8.4), на код, реализующий минимизацию численным методом, как это показано в листинге 8.16. Расчеты (которые требуют значительно большего компьютерного времени) дают тот же самый результат, что был приведен на Рисунок 8.11 и 8.12.
Примечание 5
Примечание 5
Попробуйте в расчетах листингов 8.15 и 8.16 взять иную, например, более реалистичную, априорную оценку решения (вместо использованного в них нулевого вектора х0) и посмотреть, как это повлияет на результат.
